1. Types of Compression Techniques
압축은 크게 손실 허용 압축과 손실 비허용 압축이 있음
- 손실 비허용 압축은 모든 정보를 보존함
- 손실 허용 압축은 일부 정보는 버리는 방법으로 더 나은 압축 비율을 달성할 수 있음
* 손실 압축의 예시
- 케이스 폴딩 : 대소문자 통일
- 불용어 제거 : 의미가 없는 문법적인 역할을 단어를 제거해서 핵심만 남김
- 어간 추출 : stemming. 단어의 어근을 추출해서 유사어의 의미를 단순화
* RCV1 데이터셋에 전처리 적용

- non positional postings : 텀이 등장하는 빈도 수 정보
- postitional postings : 텀이 등장하는 위치 정보를 포함
- unfiltered 전처리 안 한 원본
- no number 숫자를 제거한 경우
- case folding 대소문자 구분 없게 하는 경우
포지셔널 포스팅은 변화 없음 (대소문자 차이로 인해 분리되었던 텀들이 합쳐짐)
- 30 stop words &150 stop words
가장 많이 쓰는 30개의 불용어, 150개의 불용어를 제거한 경우
텀의 수 자체는 큰 변화가 없지만 (의미 없는 단어들)
빈도를 저장하는 non positioning 감소 (반복적인 사용)
위치를 저장하는 positioning 더 감소 (반복적인 사용마다 위치값 저장했었음)
- stemming 어간 추출
어근만 추출해서 기본형을 유지하고 나머지를 제거하니까
동일한 어근들을 하나로 통합하면 텀의 개수 감소
개별적이던 단어들의 빈도를 한 번에 처리하니까 non positiong 감소
개별적이던 단어들의 위치를 한 번에 처리하니까 positioning 감소 (위치 저장이라 더 감소)
stemming + positioning = 조금 더 많은 저장 공간이 필요하기는 하지만 위치와 문맥 검색 가능
2. Collection Statistics
* 텀 개수 추정
대부분의 문서는 일정한 크기의 사전을 가지고 있지만
대규모 문서 컬렉션일수록 사전의 크기가 큼
대규모 문서 컬렉션일수록
사전에 추가할 고유 명사가 많기 때문
(inverted index에 포함될 것이 많음)
문서 컬렉션을 통해 고유 텀 개수 M 을 추정해야함
inverted index는 위치정보를 포함하기 때문에
공간 효율을 위해 압축 필요
* heap's law
문서 컬렉션의 크기에 따라 증가하는 고유 텀의 수를 추정하는 법칙

- M 고유 텀 개수 (사전 크기)
- T 컬렉션 크기 (모든 문서들의 총 토큰 개수)
- k와 b는 상수 30-100 / 0.5
- k는 커렉션의 특성과 전처리 방식에 의해 변동
casefolding 과 stemming은 개별적으로 처리될 수 있는 텀들을 하나로 통합, 고유 텀 수 감소, k 감소
오류가 포함된 경우, 고유 텀 증가, k 증가

고유 텀 개수와 컬렉션 크기는 선형적 관계
문서의 크기가 커질수록 텀의 크기 증가 -> 대규모 컬렉션에서는 사전압축이 필요함
예시 . RCV1

사전 크기 = 전체 문서 컬렉션의 고유 텀 개수
압축 > 저장 공간 절약, 검색 효율성 향상
* zipf's law
자연어에서 일부 단어는 매우 자주 등장하고
대부분의 단어는 매우 드물게 등장함
> 문서 컬렉션 내 단어 빈도를 단어의 순위에 따라 추정 가능

Fi = i번째로 자주 등장하는 단어의 빈도
c = 정규화 상수 .. 전체 빈도를 맞추기 위함
i = 빈도 기준 단어 순위
예시
가장 자주 등장하는 단어의 빈도를 1000이라고 하면



zipf의 법칙을 두 가지 방법으로 시각화한 그래프
* 순위 i에 따른 빈도 fi 표현
오른쪽으로 갈수록 빈도가 급감
= 상위 몇 개만 높은 빈도, 나머지 대부분 낮은 빈도
= 빈도가 순위에 반비례해서 감소, 가파르게 떨어진 후 완만하게 낮아짐
* 첫 번째 그래프의 데이터를 로그 변환하여 시각화
로그 스케일로 x y축을 모두 변환하면
빈도와 순위가 선형적 관계를 나타냄을 알 수 있음
* 한글 음절 출현 빈도

3100만 개의 한글 음절 중 전체 출현 음절은 약 2200개
상위 50개의 음절이 전체 출현 빈도의 절반
가장 많이 등장하는 음절 '이'
높은 순위로 갈수록 누적 비율이 증가해서 50위에 도달하면 누적 50퍼
특정 음절이 반복적으로 많이 등장
나머지는 드물게 사용
* index compression
- 사전 크기 = 메인 메모리에 보관할 수 있을 만큼 작게
- 포스팅 크기 = 디스크 공간을 줄이면 디스크 읽는 시간 감소, 대형 검색 엔진은 메인 메모리에 많은 포스팅을 넣어서 속도 높임
- 각 포스팅은 docID로 구성되어 있다고 가정 (빈도와 위치 정보 고려 안 함)
* 인덱스 압축 > 사전 압축
- dictionary as a string 방법
- 블록 스토리지 방법
- 블록 스토리지 + 프론트 코딩
* 인덱스 압축 > 포스팅 압축
- 가변 바이트 인코딩
* 인덱스 압축 > 허프만 코드
3. Dictionary compression
* 왜 사전 압축해 ?
사전은 포스팅 보다 작은 크기인데 왜 압축하지?
- 빠른 쿼리 처리 위해 > 사전을 메모리에 보관
- 시스템을 빠르게 시작하기 위해
- 다른 앱과 효율적으로 메모리 공유하기 위해
* 사전의 자료구조

- 고정 너비 항목 배열
각 텀에 대해 고정된 공간 할당
40만 개 텀, 각각 28바이트, 전체 사전은 11.2MB
- 자료구조 구성은
텀
문서 빈도
포스팅 리스트에 대한 포인터
* Array of fixed-width entries

- 각 텀에 20 바이트 할당하는데
예시 RCV1에서 평균 텀 길이는 7.5 라서
대부분 낭비
가끔씩 20바이트 초과하는 단어는 처리 못함
- 크기가 일정해서 관리와 접근은 효율적이지만
공간 낭비 문제가 있음
* Compression : Dictionary-as-a-String
- 각 단어를 하나의 긴 문자열로 저장
- 다음 단어의 시작 위치 포인터 > 현재 텀의 끝을 간접적으로 표시
- 문서 빈도, 포스팅 리스트 포인터도 저장

예시

각 텀이 평균 8바이트인 40만 개의 텀이 있다면 3.2MB의 문자열
각 단어 가리키는 포인터에 필요한 비트 수는 로그 값

> 문서 빈도 = 4 바이트
> 포스팅 리스트 포인터 = 4바이트
> 텀 포인터 = 3바이트
> 텀 자체 = 8 바이트
총 19바이트
40만 개의 단어를 19바이트씩 = 11.2MB
* blocked storage
- 사전을 블록으로 압축
고정된 크기 k의 블록으로 그룹화해서 저장하면
k개의 텀이 하나의 블록으로 묶임
첫번째 단어에만 포인터를 할당하고 나머지는 블록 내에서 저장
- 텀 길이 정보 저장
각 텀 앞에 추가 바이트로 각 텀의 길이를 저장

* blocked storage 전체 크기 절약과 블록 크기 계산
첫번째 단어에만 포인터 > 각 블록당 k-1개 포인터 절약
단어 길이 저장하는 추가 비트 > k 낭비

k가 커질수록 더 많은 단어가 포함되니까
전체 포인터 수가 줄어들고 더 많은 공간 절약할 수 있지만
각 블록 내에서 탐색해야하니 속도 느려짐
> 적절한 k 찾는 것이 중요
압축된 사전의 크기는
{ 텀의 개수 * ( 문서 빈도 4 + 포스팅 리스트 4 + 길이 저장 1 + 텀 하나의 평균 길이 ) }
* blocked storage 없이 탐색

모든 텀을 선형 검색
단계마다 노드 개수만큼 비교하고
평균 구할 때는 노드 개수로 나눔
* blocked storage 사용하는 탐색

이진 검색으로 원하는 블록 찾고
블록 안에서 선형 검색
평균적으로 k-1번의 비교가 필요함
각 단계마다 두 번씩 비교하니까 단계 * 2 로 계산하게 됨
* blocked storage + front coding 함께 사용하는 방식

front coding
- 사전에 저장된 단어는 공통된 접두사가 있으니
공통된 접두사만 사전에 저장하고
나머지 부분만 따로 저장
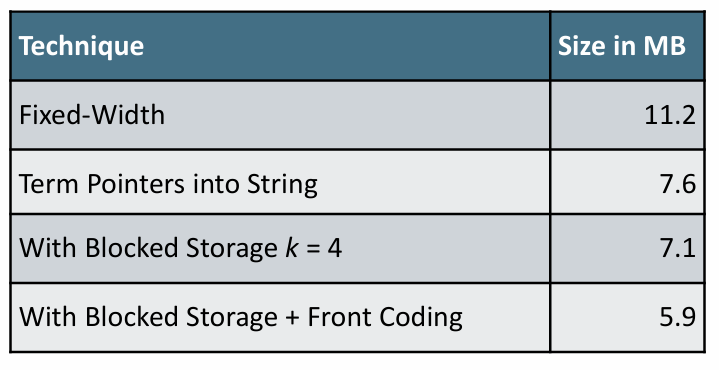
* RCV1에서의 절약 비교
4. Postings compression
* Reuters RCV1 Statistics

* Postings lists
- 포스팅 리스트는 사전보다 큼
- 문서 아이디만 들어있고 빈도나 위치 정보 없음
RCV1에서 80만 개의 문서가 각각 200개씩 6바이트의 토큰을 가지고 있으면 전체 크기는 960MB
80만개의 문서 아이디를 표현하려면
log2 800,000 ≈ 20 비트
1억 개의 포스팅이 있다면 각 포스팅은 2.5바이트를 차지하니까 250MB 필요
절대적인 문서 id가 아닌 인접한 문서 id 간의 차이를 저장하는 것이 핵심

자주 등장하는 용어는 가까운 위치의 문서에 반복적으로 등장할 가능성 높음
갭이 작은 값이 되니 더 적은 비트로 표현 가능
개별적으로 저장하는 것보다 효율적으로 사용 가능
대부분의 갭은 작은 편이라 1비트면 충분하지만
아주 가끔 등장하는 단어는 20비트 정도 필요할 수도 있음
다양한 갭 크기 때문에 같은 비트로 모든 갭을 저장하는 건 비효율적
가변 바이트 인코딩 방식 필요
* Variable Byte Encoding
각 갭을 필요한 최소 비트만 사용해서 압축
작은 갭은 짧은 바이트, 큰 갭은 여러 바이트로 저장
갭을 저장하기 위해 1바이트로 시작
각 바이트의 첫번째 비트는 continuation bit
- 0이면 다음 바이트가 이어짐
- 1이면 여기서 끝남 > 한 바이트로 전체 표현 가능함을 의미

인코딩된 포스팅 리스트는 하나의 이진수 문자열로 저장
유일하게 디코딩이 가능함 , continuation bit로 갭의 구간을 정확하게 구분 가능함
* RCV1 Compression

* Index compression summary
- 가변 바이트 인코딩 : 공간 절약, 효율적인 boolean 검색 인덱스 구축
- boolean 검색은 특정 키워드 포함된 문서 집합 찾기 유리
- 텍스트 컬렉션 크기에 비해 87퍼센트나 절약하는 가변 바이트 인코딩
- 위치 정보 포함되지 않은 인덱스
- 실제로는 위치 정보가 필요한데 추가 공간이 있어야 함
5. More on Compression
* Huffman Code
- 문자나 단어의 빈도 분포를 기반으로 각 문자에 고유한 코드를 할당하고 가변 길이 코드로 압축하는 방법
- 자주 등장하는 빈도 높은 심볼은 짧은 코드로, 드물게 등장하는 심볼은 긴 코드를 할당
- perfix property 접두사 속성
허프만 코드는 접두사 속성을 가지고 있어서 다른 어떤 코드도 다른 코드의 접두사가 되지 않도록 보장할 수 있음
즉 길이가 달라서 생길 수 있는 이슈인
긴 코드 중 일부를 고유 코드로 갖는 단어가
존재하지 않는다는 것
고유하게 해독할 수 있고 각 비트 스트림에 대해 명확하게 디코딩이 가능함
전송 오류 발생해도 일부 오류는 자동으로 해결 가능
* 허프만 코드 인코딩 방식



- 코퍼스에서 빈도를 수집하고 기록
- 수집 빈도를 기반으로 허프만 트리 (빈도 기반으로 생성하는 이진트리)를 구축
- 빈도가 낮으면 트리 깊은 곳에 긴 코드 / 빈도가 높으면 상위에 위치하니 짧은 코드
- 할당된 고유 코드로 허프만 코드 테이블 생성
- 허프만 코드 테이블을 사용해서 문자를 허프만 코드로 변환해서 인코딩
빈도에 따라 가변길이 코드가 되는 것

* 허프만 코드 디코딩 방식
- 인코딩과 같은 허프만 트리 사용해서 코드 위치 파악
- 루트부터 리프노드에 도달할 때까지 내려가면서 구한 비트스트림으로 해독
하나씩 루트부터 리프까지 반복하며 디코딩

* 허프만 코드 오류 자동 수정

접두사 속성 덕분에 디코딩 중 발생한 오류를 자동으로 감지할 수 있음
잘못된 해독을 방지하고 대부분의 경우 원래의 비트 스트림으로 돌아가서 디코딩 가능함

