1. Problems with Boolean Search
- 결과가 너무 많음
단순히 포함한다는 조건만으로 너무 많이 도출. 사용성 악화
- 조건을 충족하거나 충족하지 않는 이분법적 방식
결과의 순위 매기기 불가능. 중요한 결과와 덜 중요한 결과 구분 불가
2. 순위 기반 검색의 기초 - Scoring
* 순위 기반 검색 장점
- 검색 결과가 많더라도 정렬해서 보여줄 수 있음
- 사용자도 더 중요한 문서를 쉽고 찾게 확인 가능
* 순서 부여 방법
- 특정 쿼리와 문서가 얼마나 잘 일치하는지 문서마다 점수 부여 [0,1]
- 점수가 높을수록 관련성 높은 문서
* 쿼리와 문서의 매칭 점수 계산
- (쿼리, 문서) 쌍에 점수를 부여해서 그 점수 기반으로 관련성 계산
- 쿼리 텀이 문서에 없다면 점수는 0점
- 쿼리 텀이 문서 안에 자주 등장할수록 점수 높아짐 = 빈도 높은 것이 관련성 높은 것
3. Scoring under Boolean Search Model
* Jaccard Coefficient
- 두 집합이 겹치는 교집합 비율을 측정하는 계수 = 쿼리와 문서의 매칭 스코어 계산

- 두 교집합의 원소를 두 집합의 합집합의 원소 개수로 나누는 방식
- 0과 1 사이의 값
- 두 집합이 온전히 같은 경우 = 1
- 두 집합의 교집합이 전혀 없는 경우 = 0
예시
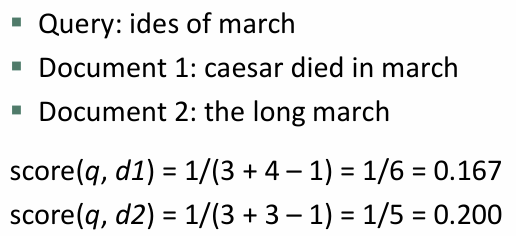
- 문서 2가 1보다 더 높은 자카드 계수를 갖는 것으로 보아
문서 2가 쿼리와 더 관련성이 높은 것
* Jaccard Coefficient 한계
- 텀 빈도 : 자주 등장하는 단어는 문서와 밀접하게 연관된 것이지만 자카드 계수는 포함 여부만 반영하는 방법
- 도큐 빈도 : 전체 컬렉션에서 드물게 등장하면 그단어에 대해 자세히 서명할 가능성이 높음
자카드 계수는 항상 빈도나 내용을 구체적으로 사용하도록 함
>> 빈도나 가치를 반영하지 않아서 중요성도 체감 비교할 수가 없고 정확도가 낮아짐
3. Vector Space Model component

* Tern Frequency
* Binary Term-Document Incidence Matrix : 이진 텀 문서 발생 행렬
- 각 문서에 특정한 텀의 포함 여부를 1과 0으로 표현 ( 포함 = 1, 안 함 = 0)
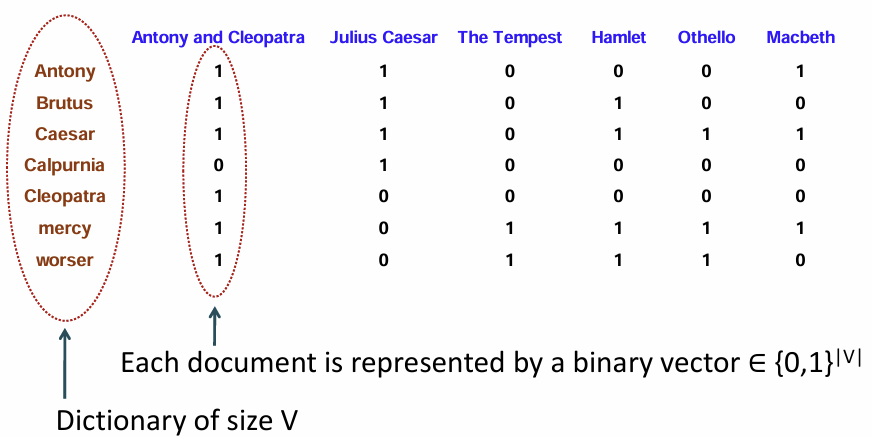
포함여부를 수로 이진적으로 표현 가능
- 각 문서는 이진 벡ㅌ로 표현 가능
- 문서는 {0,1}^|V| 에 속하는 벡터 |V|는 사전의 텀 수
* Term-Document count Matrix : 텀 문서 빈도 행렬

각 문서 내에서 특정 텀이 등장한 횟수
각 문서는 자연수 벡터로 표현 N^|V| .. 등장 빈도를 벡터의 요소로 가지게 됨
사전의 크기는 동일, 각 문서는 벡터에 의해 구체적인 용어의 빈도로 표현
* bag of words model
- 문서 내부의 단어 순서를 고려하지 않는 벡터 표현 방식
- 의미 달라도 구성이 같으면 동일한 벡터로 표현
- 단어 위치와 순서 구분 없이 , 유무와 빈도만 고려
- 문서와 쿼리의 일치도 , 간단한 유사도 계산
* term frequency TF
- 텀 빈도는 특정 문서 d에서 특정 용어 t가 등장한 횟수
- 문서와 쿼리의 일치 점수 계산시 용어 빈도로 유사도 평가
- raw TF는 빈도만 고려, 정확도에 큰 도움 x . 많이 나왔다고 더 관련 있는 것은 아님
- 로그 스케일 사용 ? 빈도에 비례한 관련성 증가 아님 ... 적당한 관련 정도
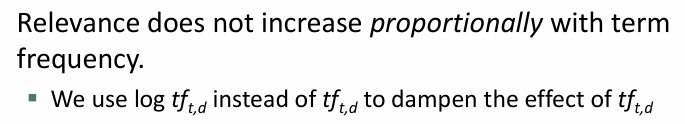
* Document Frequency
* 희귀한 단어
- 희귀한 단어는 빈도가 높은 단어보다 더 큰 정보를 줌
- 흔하지 않은 단어가 사용된 쿼리는 그 단어를 포함한 문서왁 관련되었을 가능성이 높음
- 흔하지 않은 단어에 높은 가중치를 부여

* 흔한 단어
- 자주 등장하는 단어가 양의 가중치에 대해 관련성 평가에서 높음
- 포함된 단어가 없는 것보다 높은 관련성. 하지만 단어만으로 관련되었다는 건 아님
- 빈번한 단어에는 높은 가중치, 드문 단어는 낮은 가중치
- 문서 빈도를 점수에 반영할 수 있음
- dft 특정 단어 t가 포함된 문서 d의 수
- 높을 수록 덜 중요할 수 있는 단어 (특수한 정보에 가중치 높여야 해서)
* inverse df idf
t의 문서 빈도를 반대로 계산해서 흔하지 않은 데이터에 높은 가중치를 부여
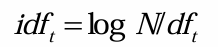
N은 컬렉션 내 문서 총 개수
로그 스케일을 사용하기 > 빈도 차이가 클 때의 영향 줄임
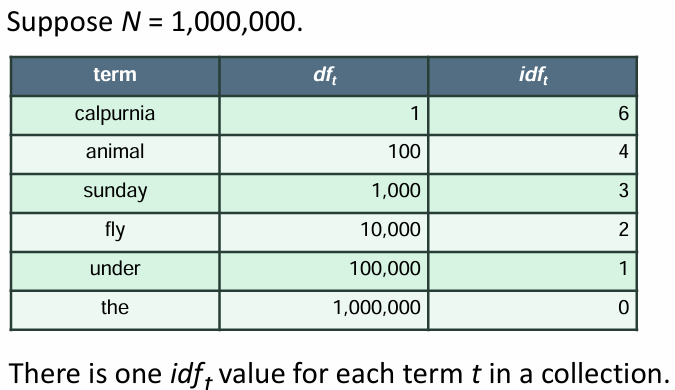
* tf-idf weight
* term frequency weight
특정 단어가 문서 내에 얼마나 자주 등장하는가
용어 빈도 tf 의 증가와 쿼리문 관련성의 증가는 비례하지 않음
이를 해결하기 위한 로그 빈도 가중치
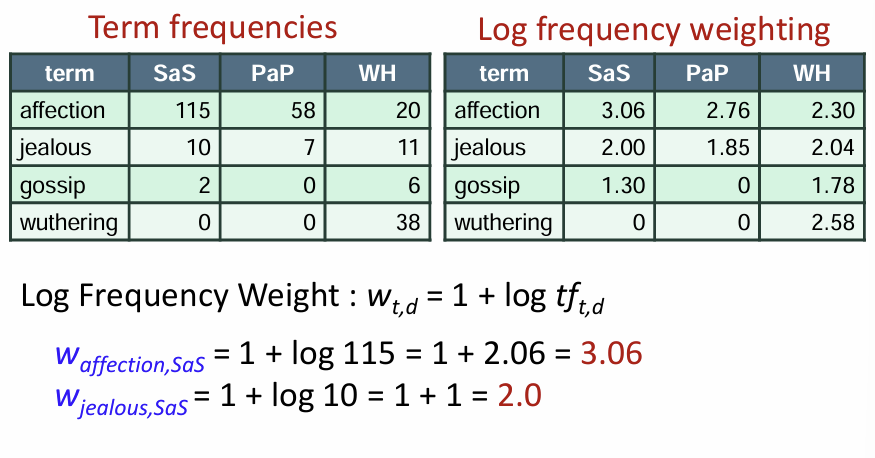
* log frequency weight

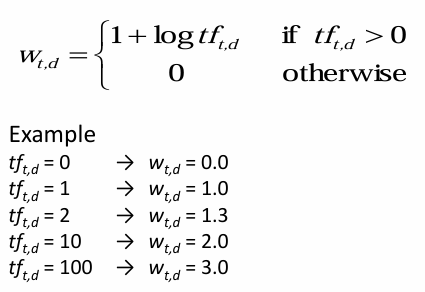
는 문서 dd 내의 용어 tft의 가중치
특정 문서 내에서의 특정 텀 빈도가 0보다 크면 로그값에 +1 을 더해서 구함
예시처럼 용어의 빈도가 높으면 가중치도 높아지지만 증가 속도는 점점 완화해서
빈도는 기하급수적으로 늘어도 가중치는 급수적으로 늘지 않음
> 로그 빈도 가중치

tf-idf (term빈도와 inverse 문서 빈도) 가중치 값을 사용해서 각 문서를 실수형 벡터로 표현한 것
특정 문서가 문서에 얼마나 자주 등장하는지
컬렉션 내에서 특정 텀이 가끔 나타날수록 높은 가중치
사전에 있는 단어 수와 동일한 차원의 실수 벡터
쿼리와 문서의 유사도
* vector space model
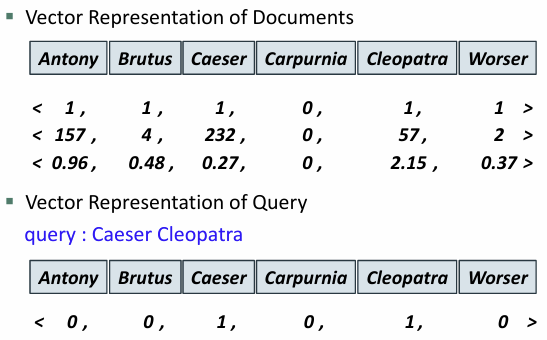
문서와 쿼리를 모두 벡터로 표현
사전에 포함된 텀의 빈도나 tf-idf 값이 벡터의 해당 위치에 반영
- 문서 내 단어의 존재 여부 0/1 벡터
- 문서 내 단어의 출현 빈도
- 문서 내 tf-idf 가중치 (빈도가 높고 드문 단어)
- 쿼리와 문서 간의 관련성
* Vector Space Model
단어가 공간의 축, 문서가 공간에서의 점과 벡터
각 단어에 속하는 값을 좌표 쌍으로
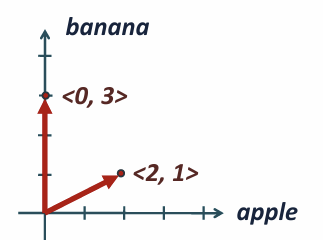
사전 크기 차원의 벡터 스페이스
대부분의 요소는 0인 sparse vector
문서와 쿼리를 동일한 벡터 공간에 투영시켜서 유사도 측정
유클리디안 거리가 가까울수록 유사도 높은 것으로 평가

* Similarity Measure
쿼리벡터와 문서벡터 사이의 거리를 계산하는 유클리디안 방식
두 벡터의 단어 분포가 유사해도 벡터 크기 때문에 거리가 커보임
문서 d에 같은 내용을 붙인 문서 d`은 크기만 크고 내용은 같음
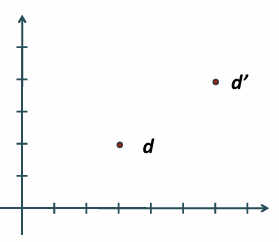
유클리디안으로는 거리가 커서 관련성이 없어 보임
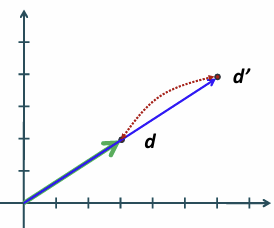
각도를 사용해서 해결
각도를 보면 0에 가까움 = 내용적으로 유사함
유사도 측정은 각도 기준으로 문서를 비교하는 것이 적절
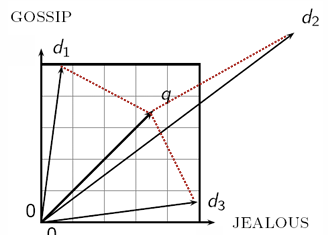
쿼리 q와 더 유사한 결과는
q와의 각도가 더 작은 쪽이 더 유사한 것
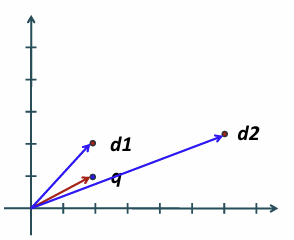
* cosine similarity
각도와 코사인 값을 이용해 쿼리와 문서 간 유사도 측정
각도가 작을수록 높은 유사도
각도를 줄이기 위해 코사인 값 사용 ( 0도일 때 1, 90도일 때 0 )
코사인 값이 클수록 각도가 작은 것이며 유사도가 높은 것
유사도 측정 방식은
각도 작은 문서에서 높은 문서 순이나
코사인 값 감소에서 증가 순으로 정렬하면
작은 문서일수록 유사도가 높음
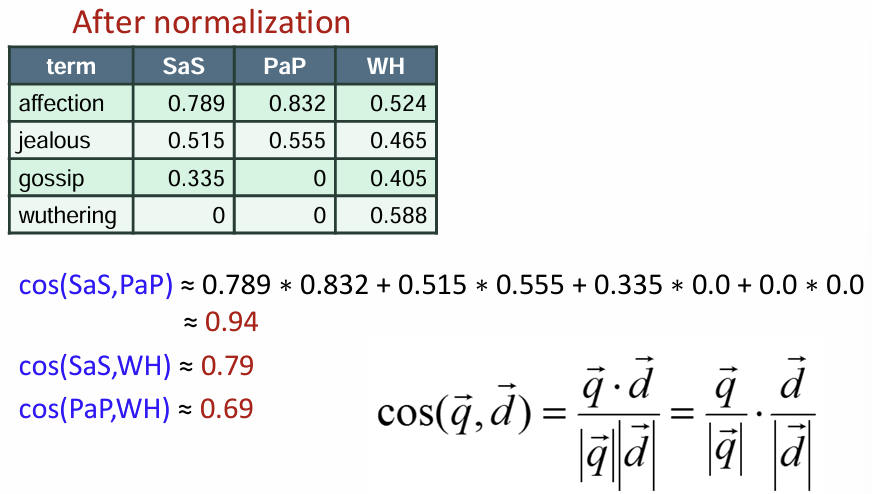
코사인 유사도 = 두 벡터 간의 내적을 두 벡터의 크기 곱으로 나눈 값
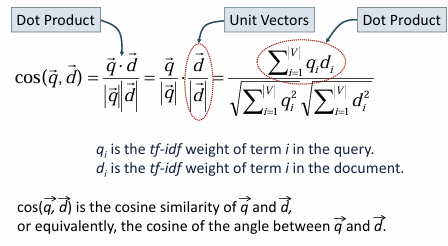
두 벡터의 내적 곱
절댓값은 각 벡터의 길이
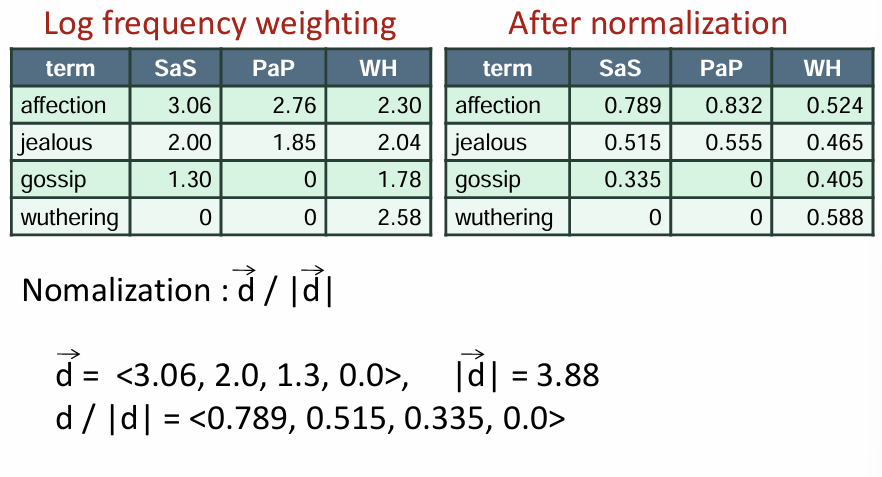
벡터의 크기를 1로 맞추기 위해 벡터 길이로 나누어서 (=벡터 정규화)
단위 벡터로 방향성만 고려하는 유사도
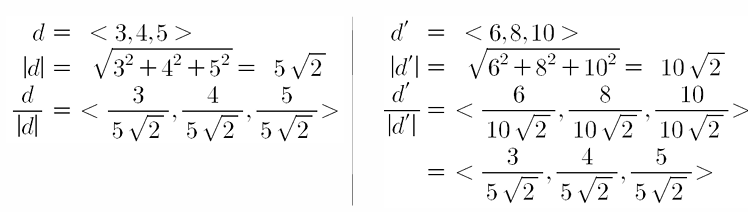
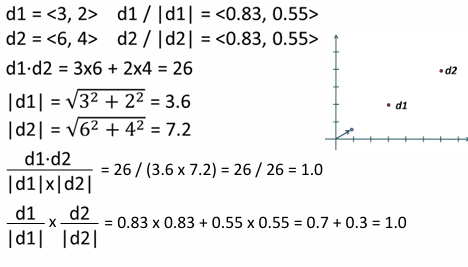
성분 값이 다르지만 정규화 해보면 결국 동일한 벡터
한 문서에 자기 자신을 추가한 다른 문서를 비교한 실험
길이 정규화는 방향성만 남김
쿼리와 두 문서 비교 예시
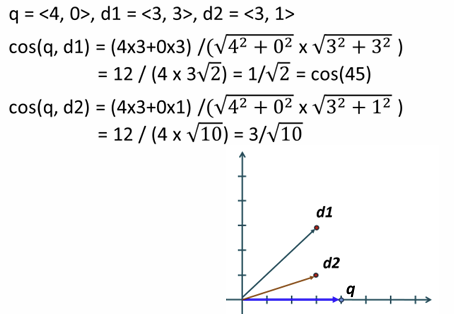
예시


'[ Computer Science ] > Information Retrieval' 카테고리의 다른 글
| [Information Retrieval] 정보 검색 5. Index compression (3) | 2024.10.31 |
|---|---|
| [Information Retrieval] 정보 검색 4. Index construction (1) | 2024.10.30 |
| [Information Retrieval] 정보 검색 3. Dictionaries and Tolerant Retrieval (0) | 2024.10.27 |
| [Information Retrieval] 정보 검색 2. The term vocabulary and postings lists (5) | 2024.10.27 |
| [Information Retrieval] 정보 검색 1. Boolean Retrieval (3) | 2024.10.27 |